But there was still considerable interest in logical systems as themselves objects of study. The crisis over the introduction of infinitistic methods into mathematics, which we have already mentioned, was still rumbling on, and Brouwer even rejected the general use of the law of the excluded middle (P 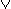P). Now on previous occasions, when mathematicians wished to provide a foundation for some new technique, they did it by an interpretation in terms of known mathematics. The classic example is the interpretation of complex numbers as pairs of real numbers. But for justifying infinite sets, there seemed to be no such way out: how can one find an interpretation for infinite sets in terms of finite ones? Hilbert's ingenious idea was to get round this by studying not the objects, but the mathematical proofs, which are always finite, even when they are about infinite sets.

Specifically, Hilbert proposed the following programme.⁴ Formal systems for various mathematical theories should be developed; thanks to the line of work culminating in Russell's logic, combined with Hilbert's own flair for axiomatization, this was straightforward. Then these should be proven consistent, i.e. that it is not possible to deduce both a theorem and its negation; in symbols P and P. Now given this, any 'concrete' theorem of the form n N. P[n] which is deducible in the system must be true. Otherwise there'd be some k N such that P[k], so any reasonable logical system will certainly be capable of proving P[k] (we assume that P[k] is simply a matter of calculation for each specific k, in particular not itself involving unbounded quantifiers). But since n N. P[n], we also have P[k], which is impossible because the system was assumed consistent. This reasoning extends to arbitrary numbers of universal quantifiers; a good example of such an assertion is Fermat's Last Theorem: x, y, z, n N. n > 2 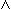xⁿ + yⁿ = zⁿ 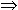x = 0 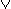y = 0.

For Hilbert, therefore, the business of proving consistency of formal theories was central. An interesting subsidiary question was the Entscheidungsproblem (decision problem): is it possible to decide questions in these formal mathematical theories purely mechanically?⁵ Hilbert and his assistants, as well as numerous other mathematicians and logicians, attacked these problems. Before long, there were negative conclusions.

First [godel-undecidable] proved his famous First Incompleteness Theorem, which says roughly that no given (consistent) formal system can ever encompass even all the truths of elementary number theory: there will always be true statements which cannot be proved in the system.⁶ Gödel's method was roughly as follows. It's easy to see that each sentence of the formal language can be allocated a unique 'Gödel number' 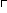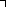, and likewise each proof -- there are after all only countably many of each, and they have a quite simple structure. Moreover, for any sensible encoding, the question of whether p is a proof of can be encoded as a representable predicate⁷ Prov(p,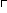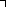), with the basic property that if then also 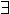p. Prov(p,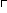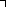). Now using a diagonalization argument, Gödel was able to exhibit a statement which (intuitively) asserts its own unprovability in the system:

p. Prov(p,)

Now if the formal system is consistent, , for if we have 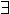p. Prov(p,) and hence . However is certainly true because it states precisely that unprovability! On the additional assumption that the system is 1-consistent, i.e. all provable existential statements are true, then also . But note that since isn't provable, adding as a new axiom retains consistency, so a formal system can be consistent yet not 1-consistent; thus the argument above that consistency implies the truth of provable universal formula cannot be sharpened. Now neither of these conclusions is fatal to Hilbert's programme:⁸ he never identified mathematics with reasoning in a particular formal system, and apparently influenced by Brouwer's critique, was prepared to dismiss existential theorems without a construction as strictly meaningless anyway.⁹ But soon after came Gödel's Second Incompleteness Theorem, which states roughly that any realistic mathematical theory, even elementary number theory, is unable to prove its own consistency. So any consistency proof of a formal system requires greater mathematical resources than available in the system, and so it certainly isn't possible to justify infinite sets finitistically. Despite the apparent promise of Hilbert's ingenious idea of using proofs, it turns out to be just as circular as using interpretations --- it's as if there's some mysterious conservation principle at work like that forbidding perpetual motion! Moreover [church-number] and [turing] showed the Entscheidungsproblem to be unsolvable even for pure first order logic, Turing by introducing his famous machines and so giving the first really convincing definition of a 'formal system'. Finally [tarski-truth] showed that arithmetical truth is not even arithmetically definable, let alone recursively enumerable.

Despite the apparent failure of Hilbert's programme, the general interest in metalogical studies has yielded many benefits and thrown new light on parts of mathematics. (Though destructive to Hilbert's programme, some of the negative results mentioned above have a profound mathematical and philosophical significance.) First order logic seems particularly interesting from a metalogical point of view: it's strong enough to express some nontrivial mathematics, yet weak enough to allow interesting metatheorems (e.g. on the existence on nonstandard models of the first order theory of reals). There turn out to be some interesting first order mathematical theories which are decidable, and this often generalizes previous results. For example, the quantifier elimination procedure for real closed fields given by [tarski-decision] is a natural generalization of well-known results on polynomial elimination such as Sturm's theorem.

John Harrison 96/2/22; HTML by 96/4/5