

In informal mathematics, our minds filter out --- even subconsciously perhaps --- troublesome degenerate cases. However in a formal treatment we must address these matters. One of the most interesting questions is: what does it mean to apply a function f to a value x outside its domain? For example, what is 0-1 in the reals?
There are numerous different approaches. The simplest is to regard f(x) for
x 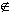 dom(f) as something
arbitrary; in effect we are expanding the domain of f but saying nothing
about the values it takes there. Alternatively, we can specify an explicit
value for values outside the domain; this approach can be exploited by
choosing a particularly convenient value. For example, if we decide
0-1 = 0, we have lots of nice unconditional theorems, like
dom(f) as something
arbitrary; in effect we are expanding the domain of f but saying nothing
about the values it takes there. Alternatively, we can specify an explicit
value for values outside the domain; this approach can be exploited by
choosing a particularly convenient value. For example, if we decide
0-1 = 0, we have lots of nice unconditional theorems, like  x
x  R. (x-1)-1 = x,
R. (x-1)-1 = x,  x
x  R. -x-1 = (-x)-1,
R. -x-1 = (-x)-1,  x, y
x, y  R. (x y)-1 = x-1 y-1 and
R. (x y)-1 = x-1 y-1 and  x
x  R. x-1
R. x-1 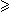 0
0
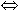 x
x 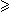 0. However some may regard these theorems
as pathological, obscene or simply untrue. Actually even if an arbitrary
value is chosen, these freak theorems show up occasionally. If we define, as
one normally would, x / y = x y-1, then 0 / 0 = 0, because
whatever 0-1 might be, it's some real number, and multiplying it
by zero gives zero! In an untyped system this problem happens less (in the
example given we wouldn't even know that 0-1
0. However some may regard these theorems
as pathological, obscene or simply untrue. Actually even if an arbitrary
value is chosen, these freak theorems show up occasionally. If we define, as
one normally would, x / y = x y-1, then 0 / 0 = 0, because
whatever 0-1 might be, it's some real number, and multiplying it
by zero gives zero! In an untyped system this problem happens less (in the
example given we wouldn't even know that 0-1  R), but does
not disappear completely.
R), but does
not disappear completely.
There is a more serious disadvantage of this scheme.
(In constructive systems there is yet another: membership of the domain may
be undecidable, so the above solution simply isn't available.) In some
mathematical contexts, writing down f(x) = y is taken to include an implicit
assertion that x  dom(f). For example, when we write:
dom(f). For example, when we write:
we take this to include an assertion that sin is in fact differentiable everywhere. But if the differentiation operator is total, it will yield a value, regardless of whether the function is actually differentiable at the relevant point. It might accidentally happen that the above equation were true even if the function weren't differentiable! This situation becomes even more serious when constructs like this are nested, e.g. in differential equations. They need to be accompanied by a long string of differentiability assumptions, which in informal usage are understood implicitly.
What are the alternatives? If we have a typed logic, then we can simply make
f(x) a typing error when x 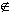 dom(f);
that is, the term is not syntactically well formed. This avoids the problems
above, but it might mean that in certain situations in analysis, the types
become complicated, since they need to excise all the singularities. It also
makes it difficult to use constructs which are permissive of point
singularities (for example, it often makes sense to integrate such
functions), and means that theorems like
dom(f);
that is, the term is not syntactically well formed. This avoids the problems
above, but it might mean that in certain situations in analysis, the types
become complicated, since they need to excise all the singularities. It also
makes it difficult to use constructs which are permissive of point
singularities (for example, it often makes sense to integrate such
functions), and means that theorems like  x
x  R. tan(x) = 0
R. tan(x) = 0 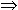
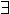 n
n  N. x = n \pi don't hold, because the antecedant is a type error
if x is one of tan's singularities.
N. x = n \pi don't hold, because the antecedant is a type error
if x is one of tan's singularities.
The most sophisticated alternative of all is to have a special logic which
allows certain terms to be undefined, as in the IMPS system [farmer-imps]. This is more or
less the same (there are some differences in detail) as taking an extra
'undefined' element on top of a conventional logic, so the result of a
function application may be this special element.29 The undefined value propagates up
through terms, so a term with an undefined subterm is itself undefined. In
IMPS, predicates involving an undefined argument become false. For
example, a = b means 'a and b are both defined and are equal'. One might
question these choices, but since a definedness operator is provided, one
can invent one's own bespoke notion of equality. In particular, IMPS
supports 'quasi-equality', where a = b means 'either a and b are both
undefined, or are both defined and equal'. In some parts of mathematics,
this is probably the usual convention, but it has some surprising
consequences, e.g. the logical equivalence x = y 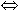 x - y = 0 is false for quasi-equality. One could even
invent circumstances in which
x - y = 0 is false for quasi-equality. One could even
invent circumstances in which  x
x
 R. (x2 - 1) / (x - 1) = x + 1 was desired behaviour
(wherever the two sides are both defined, they are equal). Actually, [freyd-allegories] uses a
special asymmetric 'Venturi tube' equality meaning 'if the left is defined
then so is the right and they are equal'.
R. (x2 - 1) / (x - 1) = x + 1 was desired behaviour
(wherever the two sides are both defined, they are equal). Actually, [freyd-allegories] uses a
special asymmetric 'Venturi tube' equality meaning 'if the left is defined
then so is the right and they are equal'.
We spoke above of the informal convention in
mathematics. It seems that many authors are actually doing something like
defining the equality predicate contextually. This seems surprising when
equality is considered such a basic thing, but the conclusion is hard to
avoid when one sees phrases like 'if y is the unique value with (x,y)  f, we write f(x) =
y'. This isn't specific to a foundational discussion of function
application; many analysis texts do similar things for the limiting
operation, for example. In fact it's rather common to see mathematics books
make 'conditional' definitions --- 'if x is ..., then we define f(x) = E[x]'
rather than just 'we define f(x) = E[x]' --- again, there is probably a wish
to have certain contextual information carried around with the definition.
Set theory texts are occasionally more explicit, e.g. they may say 'f(x) is
the (unique) y such that (x,y)
f, we write f(x) =
y'. This isn't specific to a foundational discussion of function
application; many analysis texts do similar things for the limiting
operation, for example. In fact it's rather common to see mathematics books
make 'conditional' definitions --- 'if x is ..., then we define f(x) = E[x]'
rather than just 'we define f(x) = E[x]' --- again, there is probably a wish
to have certain contextual information carried around with the definition.
Set theory texts are occasionally more explicit, e.g. they may say 'f(x) is
the (unique) y such that (x,y)  f'. One formalization of this is the descriptor term
f'. One formalization of this is the descriptor term
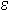 y. (x,y)
y. (x,y)  f, but,
depending on the precise semantics of the descriptor and the logic, this can
mean different things.
f, but,
depending on the precise semantics of the descriptor and the logic, this can
mean different things.



 John Harrison
96/2/22; HTML by
John Harrison
96/2/22; HTML by  96/4/5
96/4/5