As de Bruijn says, we want to use abbreviations for common patterns of inference. The patterns of inference which are common may, of course, depend on the particular piece of mathematics being formalized, so it's desirable to allow ordinary users to extend the inference rules system, while at the same time being confident that only correct inferences are made. LCF realizes this desire exactly. Arbitrary programs can be written to prove a fact, perhaps from several premisses; the only restriction being that although terms and types may be built up, and theorems decomposed, quite arbitrarily, theorems can only be created by the primitive inference rules. It is not necessary that the program should prove some fact in a uniform way; it might, depending on the form of the fact to be proved, invoke one of several quite different algorithms. This is not always appreciated by outsiders, as one can see from the following assertion by [davis-schwartz]: 'an LCF tactical is limited to a fixed combination of existing rules of inference'. It is not, and therein lies the value of the LCF approach as compared with simple macro languages.³¹

In principle, whenever there is a class of proofs of the form A₁, ..., A_n B, then a corresponding inference rule is derivable: we can write a HOL derived rule which implements that class of derivations. If nothing else, we can blindly search all possible proofs till we arrive at this theorem. But of course that's not practical, so really one is interested in cases where there is a natural, feasible algorithm for finding the derivation. For example, consider the class of theorems where is a propositional tautology. We can start from any given way of deciding that a formula is a tautology (e.g. the use of truth tables), and attempt to translate this algorithm into a version which performs proof by primitive inference.

Just how practical is this? At first sight, when one considers the enormous number of special-purpose algorithms and the likely cost of generating formal proofs, it looks completely impractical; [armando-building] opine that it 'turns out to be both unnatural and ineffective' (though apparently on general grounds rather than on the evidence of having tried). And indeed, not all LCF systems have stuck with the rigorous policy of decomposing all inference to the primitives. For example, Nuprl users have shown no particular compunction about throwing in extra proof procedures for linear arithmetic or tautologies when the need arises. However these human factors do not provide hard evidence about feasibility.³² The users of the HOL system at least have ploughed their own furrow, implementing a variety of quite sophisticated proof techniques, all decomposing to primitive inferences. We are now able to step back and survey the lessons. There are two questions: whether it is a reasonably tractable task for the programmer, and whether the resulting program is acceptably efficient (the latter question is closely related to our previous discussion of feasibility). It has emerged that many HOL derived rules are feasible and practical. We can identify two clear reasons why the apparent difficulties are often not really serious.

First, complex patterns of inference can be encoded as single theorems, proved once and for all. These can then be instantiated for the case in hand rather cheaply. This idea has long been used by HOL experts; for an early example see [melham-tydef]. A more recent, and complex, example is the following [harrison-hol93] justifying a step in a quantifier-elimination procedure for the reals; it states that a finite set (list) of polynomials are all strictly positive throughout an interval if and only if they are all positive at the middle of the interval and are nonzero everywhere in it.

l, a, b. a < b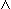
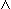(x. a < x x < b 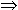FORALL (POS x ) l)
= a < b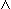
FORALL (POS (({a + b})/({2})) ) l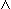
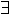x. a < x 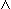x < b 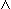EXISTS (ZERO x ) l

Many special-purpose algorithms can be understood as a natural process of transformation. It is not difficult to store theorems which justify the individual steps; the algorithm can often be implemented almost as one would do without the primitive inference steps, and generally with a modest linear slowdown (there are a few delicate points over the efficiency of equality testing, but that's more or less true). This applies, for example, to HOL's implementation of rewriting and definition of inductively defined relations, as well as numerous special-purpose rules that users write in the course of their work, e.g. the conversion to differentiate algebraic expressions by proof described by [harrison-fmsd94].

Second, many other proof procedures rely heavily on search. For example, automated theorem provers for first order logic often perform thousands, even millions, of steps which are purely devoted to finding a proof. Once the proof is found, it is usually short, and can be translated into HOL inferences very easily, and proportionately the burden of translating to primitive inferences is practically nil; performance can match any other system, written in the same language. There are now several tools for first order automation in HOL, the earliest being due to [kumar-faust]; they all work in this way. Actually, it's not even necessary to perform proof search in the same language or the same machine; [harrison-thery2] describe the use of the Maple computer algebra system as an oracle, to find solutions to integration and factorization problems which can then be checked fairly efficiently inside HOL.

The combination of these two factors is enough to make it likely that any inference patterns likely to occur in normal mathematics can be done acceptably efficiently as LCF-style derived rules. Even for the special algorithms often used in system verification, it's not inconceivable that an LCF implementation would be fast enough in practice; for example [boulton-thesis] describes an implementation of a linear arithmetic decision procedure. A particularly difficult case is the BDD algorithm, to which neither of the above factors applies with great strength; however a HOL implementation has been produced by [harrison-cj95] which exhibits only a linear slowdown, albeit a large one (around 50).

There is another potential difficulty to discuss. As pointed out by [pollack-extensibility], there are other valid inference rules, which he calls admissible to distinguish them from the derivable rules above. 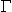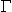These are ones where the process of passing from A₁, ..., A_n to B cannot be done in a natural way based only on the statements of the A_i, but requires more information, in particular about how the A_i were proved.³³ Two examples which come to mind are the Deduction theorem for Hilbert-style proof systems, which allows passage from p q to p 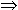q, and 'Skolemization' in certain systems of intuitionistic logic, allowing a step from x. 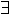y. P[x,y] to 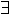f. x. P[x,f(x)]. Both these can be justified by a transformation on the proofs of the hypothesis, but apparently not easily just from the form of the hypothesis. Our answer to this question is: there seem to be no relevant instances of the phenomenon for 'reasonable' logics (such as HOL), and if this ever does become a problem, it is possible to store proofs too as concrete objects with the theorems. Various constructive systems are already capable of doing that, since extracting programs from proofs is one of the key ideas underlying such systems. Of course there is a question mark over whether such manipulations on proofs are computationally practical.

John Harrison 96/2/22; HTML by 96/4/5