

Here we list some of the logical symbols we use in the paper, for the
benefit of readers who aren't used to symbolism at all, or are used to
different symbols. Binary connectives bind according to their order in the
table below,  being the strongest.
The scope of a quantifier, lambda-abstraction or descriptor is as far to the
right of the dot as possible. For example
being the strongest.
The scope of a quantifier, lambda-abstraction or descriptor is as far to the
right of the dot as possible. For example  x.
P[x]
x.
P[x] 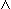 Q[x]
Q[x] 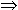 R[x] is parsed as
R[x] is parsed as  x.
((P[x]
x.
((P[x] 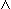 Q[x])
Q[x]) 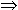 R[x]). We make a fuss
about this last point because some books adopt the opposite convention. The
table below gives the symbolic expressions we will use.
R[x]). We make a fuss
about this last point because some books adopt the opposite convention. The
table below gives the symbolic expressions we will use.
| Symbol | Other notations | English reading |
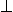 | F, 0 | false |
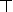 | T, 1 | true |
 P P | ~ P, -P | not P |
P 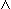 Q Q | P & Q, P . Q, P Q | P and Q |
P 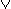 Q Q | P | Q, P or Q, P + Q | P or Q |
P 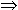 Q Q | P
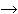 Q, P Q, P 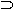 Q Q | P implies Q |
P 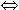 Q Q | P ~ Q, P
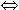 Q Q
| P if and only if Q |
 x. P x. P
| ( x) P, x) P,
 x:P, (x):P, x:P, (x):P,
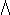 x:P x:P | for all x, P |
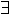 x. P x. P
| (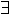 x) P, x) P,
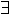 x:P, (Ex):P, x:P, (Ex):P, 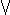 x:P x:P | there exists an x such that P |
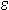 x. P x. P
| some x such that P | |
 x. P x. P
|  x.: P x.: P | the unique x such that P |
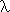 x. t x. t
| x 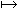 t, [x] t t, [x] t | the function of x which yields t |
 P P | P is deducible (in a formal system) | |



 John Harrison
96/2/22; HTML by
John Harrison
96/2/22; HTML by  96/4/5
96/4/5