

In formalizing mathematics, we must use our judgement to define informal
constructs in terms of formal ones, which is merely an extreme case of
defining non-rigorous concepts rigorously. This isn't always easy, but there
can be surprising successes --- for example, before Turing it would have
seemed implausible that a simple and rigorous formalization of 'computable'
could be given. For a good historical precedent, consider how Bolzano and
Weierstrass arrived at rigorous ' -
-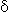 ' definitions of
notions like limits and continuity. We may have our own intuitive ideas of
what a continuous function is: perhaps one whose graph we can draw without
taking our pencil from the graph paper, or which passes through all
intermediate values. But the definition of continuity which is now standard
is neither of these; we say a function f:R
' definitions of
notions like limits and continuity. We may have our own intuitive ideas of
what a continuous function is: perhaps one whose graph we can draw without
taking our pencil from the graph paper, or which passes through all
intermediate values. But the definition of continuity which is now standard
is neither of these; we say a function f:R 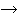 R is continuous on R iff:
R is continuous on R iff:
 x
x  R.
R. 
 > 0.
> 0. 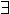
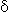 >
0.
>
0.  x'. |x - x'| <
x'. |x - x'| < 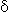
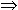 |f(x) - f(x')| <
|f(x) - f(x')| <

In what sense is this or any other formal definition 'right'? Why not take the intermediate value property (called 'Darboux continuity') instead?
 x, x', z
x, x', z  R. x < x'
R. x < x' 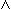 f(x)
< z < f(x')
f(x)
< z < f(x') 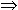
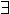 w. x < w < x'
w. x < w < x' 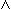 f(w) = z
f(w) = z
Such worries can be allayed when the various plausible-looking formalizations
are all provably equivalent. For example, the various definitions of
computability in terms of Turing machines, Markov algorithms, general recursive
functions, untyped 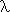 -calculus, production systems and so forth all
turned out so. But here this is not the case: continuity implies Darboux
continuity but not conversely.15 The usual definition of continuity
has probably won out because it is intuitively the most satisfying, leads to
the tidiest theory or (most likely) admits the most attractive generalization
to other metric and topological structures. But note that it also led to the
counterintuitive pathologies of real analysis which, as we have already
remarked, caused such disquiet once. This example well illustrates how
formalization can be a difficult and creative task, and that the formal version
of a concept can take on an unexpected life of its own. However, since
present-day mathematics is mostly quite rigorous, the final step to complete
formalization shouldn't usually be so problematical.
-calculus, production systems and so forth all
turned out so. But here this is not the case: continuity implies Darboux
continuity but not conversely.15 The usual definition of continuity
has probably won out because it is intuitively the most satisfying, leads to
the tidiest theory or (most likely) admits the most attractive generalization
to other metric and topological structures. But note that it also led to the
counterintuitive pathologies of real analysis which, as we have already
remarked, caused such disquiet once. This example well illustrates how
formalization can be a difficult and creative task, and that the formal version
of a concept can take on an unexpected life of its own. However, since
present-day mathematics is mostly quite rigorous, the final step to complete
formalization shouldn't usually be so problematical.



 John Harrison
96/2/22; HTML by
John Harrison
96/2/22; HTML by
 96/4/5
96/4/5