We shouldn't be too dogmatic about what is the 'natural' formalization of informal (or preformal) notions. We do not claim that reductionism always reflects the most interesting aspects of mathematics; in fact as Mac Lane has remarked, it can give a rather one-sided view of mathematical activity. But this is no more a problem than the fact that formal grammar rules do not contribute to poetry. And we should certainly avoid regarding the implementability of mathematical concepts as sets, say, as constituting some kind of ontological discovery -- this view is rightly parodied by [benacerraf]. Rather, it's an interesting and surprising practical discovery about the flexibility of set theory, to be compared with Gentzen's discoveries about the flexibility of a simple inferential apparatus. (At the same time the reduction is not without philosophical significance: in particular the consistency of practically all of mathematics can be reduced to the problem of whether ZF set theory is consistent, so our foundational concerns tend to come home to roost in set theory.)

With these disclaimers in mind, let's look now at a few examples of how the basic concepts of formal systems can be used to define other notions. We'll arrange these in order of the amount of light they throw on the informal concept (in the opinion of the present author).

1. Kuratowski showed that ordered pairs could be defined by (x,y) = {x,{x,y}} (a more complicated alternative was earlier proposed by [wiener-pair]). However it seems that this tells us nothing new about ordered pairs, except for pathological theorems which we don't want anyway. Indeed in stratified set theories like Quine's NFU [holmes-naive] and work in coinductive definitions [paulson-coalgebra], another definition is normally used.

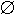2. von Neumann's definition of the ordinals is often used to identify the natural numbers with the set omega of finite ordinals. This means that 0 = , 1 = {0}, 2 = {0, 1} etc. Although this is also quite arcane and ad hoc (do we really want 0 1?) it does have the benefit of streamlining and simplifying a lot of theorems about natural numbers and integrating them with their counterparts for ordinals and cardinals. Indeed [halmos-ba] finds the use of 2 as a canonical 2-element set sufficiently convenient to remark on it.

3. We identify sequences indexed by the natural numbers, as used for example in real analysis, with functions out of N. It's quite conceivable that one could work with sequences without making explicitly the realization that the two concepts are identical. However it seems there are no reasons for forcing a distinction, so here the formalization is a unifying and simplifying force. In fact, this observation seems first to have appeared with Peano's ' Formulaire', so it provides a concrete example of a mathematical development being stimulated by a programme of formalization.

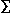4. Variable binding constructs (extensional ones anyway), such as summation, integration and differentiation, can all be regarded as a higher order operator applied to a lambda-term. That is, _i=1¹⁰ i is 'really' SUM(1,10,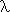i. i) while the derivative notation d/(dx) x² is really DIFF(x,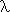x. x²). This really is a useful clarifying force, confronting us with awkward constructs where the everyday notation confuses free and bound variables or a function with its value. For example, in the example above of Leibniz notation for differentiation, x has both free and bound occurrences.¹⁶ The breakdown to a lambda-term has helped to make this explicit. Though the Leibniz notation is familiar, it can be awkward and is often abandoned in advanced or multivariate work. For example, try writing the Chain Rule for differentiation using just the Leibniz notation! Other notations like f'(x) seem better for such purposes, but can still lead to confusion; the author has witnessed a heated debate on sci.math among good mathematicians over whether f'(g(x)) denotes the derivative of f evaluated at g(x) (this view seems most popular) or the derivative of f o g evaluated at x ('the prime notation (f') is a shorthand notation for derivative of a univariate function with respect to the free variable.')

John Harrison 96/2/22; HTML by 96/4/5