

The process of formalization must also incorporate a critical aspect when the need arises. Certain concepts which do not admit a satisfactory formalization may have to be jettisoned, modified, or relegated to the status of heuristic aids. It is hoped that this procedure leads only to superficial notational rigorization of mathematics, rather than the mutilation of important ideas and principles.
In a computer-based system especially, it's vital to avoid all notational ambiguities. Generally, the more flexible grammatical rules are, the more complicated they are too, and the more scope they leave for misunderstanding. A balance needs to be struck. For example, most people would agree that different precedences for binary operators are a good idea, but sometimes the precedences chosen can confute people's expectation. (For example in C the bitwise AND operator ' &' binds less tightly than the equality relation ' ==', a historical accident that must have caused innumerable programming errors.) But many people do not accept the arbitrary solution of the 'dangling else' problem,17 and many languages strive to avoid it in different ways. Another controversial question is the overloading of operators, e.g. the use of + for addition of both integers and floating point values.
A good example of abuse of notation in mathematics books is the use of
f-1 to denote both the inverse function of f, i.e. f-1
(f(x)) = x, and the preimage of a subset of f's range, i.e.
f-1(S) = {x | f(x) 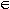 S }. Books usually glibly observe that the notation
is not confusing because the former meaning is only used if f is bijective,
and then the image of S under f-1 is the same as the preimage of
S under f. That's true, but there's quite a sophisticated use of context to
determine whether f is bijective, and at the very least we need some kind of
'typechecking' to resolve whether f-1 is being applied to an
element of ran f or a subset. Another notation that is usually clear
intuitively but hard to describe formally is indexed set abstraction { f(x)
| P[x] }, for example { (m,n) | m + n = p }. In general, it's not easy to
determine whether variables are supposed to be bound by the construct or not
(for example, the above example is probably intended to bind both m and n,
but if m means something outside, that might no longer be so.) Mathematics
contains other confusions between free and bound variables and between
constants and variables. There is a popular disclaimer attached to the
general quartic equation: 'a x4 + b x3 + c
x2 + d x + e where e is not necessarily the base of natural
logarithms'. And we have already discussed the problems of the Leibniz
derivative notation. Another popular abuse of language is to use X to refer
to the poset (X,
S }. Books usually glibly observe that the notation
is not confusing because the former meaning is only used if f is bijective,
and then the image of S under f-1 is the same as the preimage of
S under f. That's true, but there's quite a sophisticated use of context to
determine whether f is bijective, and at the very least we need some kind of
'typechecking' to resolve whether f-1 is being applied to an
element of ran f or a subset. Another notation that is usually clear
intuitively but hard to describe formally is indexed set abstraction { f(x)
| P[x] }, for example { (m,n) | m + n = p }. In general, it's not easy to
determine whether variables are supposed to be bound by the construct or not
(for example, the above example is probably intended to bind both m and n,
but if m means something outside, that might no longer be so.) Mathematics
contains other confusions between free and bound variables and between
constants and variables. There is a popular disclaimer attached to the
general quartic equation: 'a x4 + b x3 + c
x2 + d x + e where e is not necessarily the base of natural
logarithms'. And we have already discussed the problems of the Leibniz
derivative notation. Another popular abuse of language is to use X to refer
to the poset (X,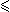 ), leaving the ordering implicit.
[bourbaki-sets] has already
shown a good way out here: we can take the ordering relation as primitive,
replacing the reflexivity property in the usual definition of partial order
by x
), leaving the ordering implicit.
[bourbaki-sets] has already
shown a good way out here: we can take the ordering relation as primitive,
replacing the reflexivity property in the usual definition of partial order
by x 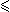 y
y 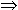 x
x 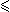 x
x 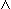 y
y 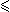 y, recovering X if desired as { x | x
y, recovering X if desired as { x | x 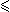 x }.18
x }.18
It is quite possible that the critical faculties of the formalizer may go well beyond cleaning up sloppy notation. The formalizer may merely want to reconstruct existing mathematics in a formal framework, but may prefer to develop a new (better?) mathematics. It is clear that Zermelo had the former aim in mind when he introduced his set theory,19 but not all logicians and philosophers of mathematics take such a respectful view of existing practice. In particular, among many mathematical logicians there is a strong tendency to be:
Perhaps the formalization of mathematics provides an ideal opportunity to make a clean break, just as when one rewrites a program in a new language, it's a good opportunity to make some revisions. On the other hand, if we hope to interest many mathematicians, we need to accommodate existing mathematics. We are already trying to wreak one revolution by making the mathematicians formalize their work. Surely one revolution at a time is enough! And, if we take a crude measure of productivity, it seems much easier to develop classical mathematics than constructive mathematics. Formalization is not a mechanical and trivial process, but a significant research problem in itself. If we add to that the new problems which arise, say, when trying to constructivize mathematics, then we are probably going to find the process particularly difficult. Experience of Nuprl researchers indicates that formalization of constructive analysis and algebra is difficult, since the existing treatments leave a lot unsaid. And sometimes the textbook approaches do not scale up well in practice; for example, maintaining the standard Bishop 1/n bound on convergence of Cauchy sequences is very tedious when doing nontrivial things with constructive reals (like solving differential equations). But on the positive side, this can be seen as an interesting motivation for new research!
Of course to some extent classical and constructive mathematics can coexist. The approach of [bishop-bridges] to constructive analysis has the merit of being compatible with classical analysis.21 But it is more complicated: one classical theorem often splits into several constructive versions (classically equivalent); the classicist may regard this as meaningless clutter. And certain constructive systems are actually in conflict with classical analysis and with each other --- [bridges-richmann] give an interesting comparative survey. So though it sounds very nice to say 'if a theorem can conveniently be proved constructively, then prove it constructively, and it can still be used classically', the real situation is more complicated. Those without constructive interests are unlikely to make the additional effort, anyway.



 John Harrison 96/2/22;
HTML by
John Harrison 96/2/22;
HTML by
 96/4/5
96/4/5